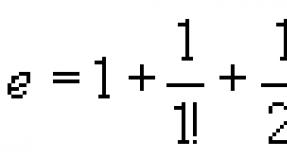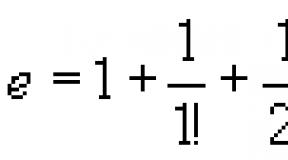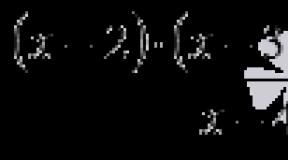Трансцендентное число

число (действительное или мнимое), не удовлетворяющее никакому алгебраическому уравнению (См. Алгебраическое уравнение) с целыми коэффициентами. Таким образом, Т. ч. противопоставляются алгебраическим числам (См. Алгебраическое число). Существование Т. ч. впервые установил Ж. Лиувилль (1844). Отправной точкой для Лиувилля служила его теорема, согласно которой порядок приближения рациональной дроби с данным знаменателем к данному иррациональному алгебраическому числу не может быть произвольно высоким. Именно, если алгебраическое число а удовлетворяет неприводимому алгебраическому уравнению степени n с целыми коэффициентами, то для любого рационального числа с зависит только от α ). Поэтому, если для заданного иррационального числа α можно указать бесконечное множество рациональных приближений, не удовлетворяющих приведённому неравенству ни при каких с и n (одних и тех же для всех приближений), то α есть Т. ч. Пример такого числа даёт:

Другое доказательство существования Т. ч. дал Г. Кантор (1874), заметив, что множество всех алгебраических чисел счётно (то есть все алгебраические числа могут быть перенумерованы; см. Множеств теория), тогда как множество всех действительных чисел несчётно. Отсюда следовало, что множество Т. ч. несчётно, и далее, что Т. ч. составляют основную массу среди множества всех чисел.

Важнейшая задача теории Т. ч. - это выяснение того, являются ли Т. ч. значения аналитических функций, обладающих теми или иными арифметическими и аналитическими свойствами при алгебраических значениях аргумента. Задачи этого рода принадлежат к числу труднейших задач современной математики. В 1873 Ш. Эрмит доказал, что Неперово число

В 1882 немецкий математик Ф. Линдеман получил более общий результат: если α - алгебраическое число, то е α - Т. ч. Результат Липдемана был значительно обобщён немецким математиком К. Зигелем (1930), доказавшим, например, трансцендентность значения широкого класса цилиндрических функций при алгебраических значениях аргумента. В 1900 на математическом конгрессе в Париже Д. Гильберт среди 23 нерешенных проблем математики указал на следующую: является ли трансцендентным числом α β , где α и β - алгебраические числа, причём β - иррациональное число, и, в частности, является ли трансцендентным число е π (проблема трансцендентности чисел вида α β была впервые в частной форме поставлена Л. Эйлер ом, 1744). Полное решение этой проблемы (в утвердительном смысле) удалось получить лишь в 1934 А. О. Гельфонд у. Из открытия Гельфонда, в частности, следует, что все десятичные логарифмы натуральных чисел (то есть «табличные логарифмы») суть Т. ч. Методы теории Т. ч. прилагаются к ряду вопросов решения уравнений в целых числах.

Лит.: Гельфонд А. О., Трансцендентные и алгебраические числа, М., 1952.

Большая советская энциклопедия. - М.: Советская энциклопедия . 1969-1978 .

Смотреть что такое "Трансцендентное число" в других словарях:

Число, не удовлетворяющее никакому алгебраическому уравнению с целыми коэффициентами. Трансцендентными числами являются: число??3,14159...; десятичный логарифм любого целого числа, не изображаемого единицей с нулями; число е=2,71828... и др … Большой Энциклопедический словарь

- (от лат. transcendere переходить, превосходить) это вещественное или комплексное число, не являющееся алгебраическим иными словами, число, которое не может быть корнем многочлена с целыми коэффициентами. Содержание 1 Свойства 2… … Википедия

Число, не удовлетворяющее никакому алгебраическому уравнению с целыми коэффициентами. Трансцендентными числами являются: число π = 3,14159...; десятичный логарифм любого целого числа, не изображаемого единицей с нулями; число е = 2,71828... и др … Энциклопедический словарь

Число, не удовлетворяющее никакому алгебр. ур нию с целыми коэффициентами. Т. ч. являются: число ПИ = 3,14159...; десятичный логарифм любого целого числа, не изображаемого единицей с нулями; число е = 2,71828... и др … Естествознание. Энциклопедический словарь

Число, не являющееся корнем никакого многочлена с целыми коэффициентами. Областью определения таких чисел являются ноля действительных, комплексных и р адических чисел. Существование и явные построения действительных Т. ч. обосновал Ж. Лиувилль… … Математическая энциклопедия

Уравнение, не являющееся алгебраическим. Обычно это уравнения, содержащие показательные, логарифмические, тригонометрические, обратные тригонометрические функции, например: Более строгое определение таково: Трансцендентное уравнение это уравнение … Википедия

Число, приближенно равное 2,718, которое часто встречается в математике и естественных науках. Например, при распаде радиоактивного вещества по истечении времени t от исходного количества вещества остается доля, равная e kt, где k число,… … Энциклопедия Кольера

E математическая константа, основание натурального логарифма, иррациональное и трансцендентное число. Иногда число e называют числом Эйлера (не путать с т. н. числами Эйлера I рода) или числом Непера. Обозначается строчной латинской буквой «e».… … Википедия

E математическая константа, основание натурального логарифма, иррациональное и трансцендентное число. Иногда число e называют числом Эйлера (не путать с т. н. числами Эйлера I рода) или числом Непера. Обозначается строчной латинской буквой «e».… … Википедия

Слово «трансцендентный» обычно ассоциируется с трансцендентальной медитацией и разнообразной эзотерикой. Но чтобы употреблять его правильно, нужно как минимум отличать его от термина «трансцендентальный», а как максимум - вспомнить его роль в работах Канта и других философов.

Это понятие произошло от латинского transcendens - «переступающий», «превосходящий», «выходящий за пределы». В целом он обозначает то, что принципиально недоступно для эмпирического познания или не основано на опыте. Предпосылки термина возникли еще в философии неоплатонизма - основатель направления Плотин создал учение о Едином - всеблагом первоначале, которое невозможно познать ни усилием мысли, ни с помощью чувственного опыта. «Единое не есть сущее, но родитель его» - объясняет философ.

Полнее всего термин «трансцендентный» был раскрыт в философии Иммануила Канта, где он использовался для характеристики , существующих независимо от сознания и действующих на наши органы чувств, оставаясь при этом принципиально непознаваемыми, как на практике, так и в теории. Противоположность трансцендентности - : она означает либо неотъемлемость, внутреннюю связь какого-либо качества объекта с самим объектом, либо познаваемость объекта на личном опыте. Например, если предположить, что Вселенная создана по какому-то высшему замыслу, сам замысел для нас трансцендентен - мы можем только строить гипотезы о нем. Но если этот замысел существует в действительности, его последствия для нас имманентны, проявляясь в физических законах и обстоятельствах, в которые мы попадаем. Поэтому в некоторых теологических концепциях Бог трансцендентен и находится вне созданного им бытия.

Некоторые вещи-в-себе все же доступны априорному познанию: например, пространство и время, идеи Бога, добра и красоты, логические категории. То есть трансцендентальные объекты - это, образно говоря, «предустановленные по умолчанию» в нашем разуме

Представление о трансцендентности существует и в математике: трансцендентное число - это число, которое не может быть вычисленным при помощи алгебры или выраженным алгебраически (то есть, не может быть корнем многочлена с целыми коэффициентами, не тождественного нулю). В их число входят, например, числа π и e.

Понятие, близкое к «трансцендентному», но иное по значению - «трансцендентальное». Изначально оно обозначало просто область отвлеченных умственных категорий, а впоследствии его развил Кант, попав в собственную ловушку: построить философскую систему только на эмпирических данных оказалось невозможно, а никаких других источников опыта, кроме эмпирики он не признавал. Чтобы выкрутиться, философу пришлось допустить, что некоторые вещи-в-себе все же доступны априорному познанию: например, пространство и время, идеи Бога, добра и красоты, логические категории. То есть трансцендентальные объекты - это, образно говоря, «предустановленные по умолчанию» в нашем разуме - при этом информация о них существует сама по себе и не следует из нашего опыта.

Существует и еще одно родственное понятие - трансценденция. В широком смысле слова оно означает переход границы между двумя разнородными областями, в особенности переход из сферы посюстороннего в сферу потустороннего, трансцендентного. Для простоты возьмем пример из фантастики: параллельный мир для обычного человека - трансцендентное явление. Но когда герой попадает в этот параллельный мир или каким-то образом оказывается способен его воспринимать, это трансценденция. Или более сложный пример из экзистенциальной философии: Жан-Поль Сартр считал, что человек трансцендентен, поскольку он выходит за рамки любого возможного собственного опыта: мы можем изучать себя и окружающий мир с разных сторон, но никогда даже не приблизимся к полному познанию себя. Но одновременно человек обладает способностью к трансценденции: он трансцендирует любую вещь, придавая ей какое-либо значение. Трансценденция - важный элемент и в религии: она помогает человеку освободиться от своей материальной природы и прикоснуться к чему-то запредельному.

Из философии понятие трансцендентальности перекочевало и в психологию: швейцарский психолог Карл Юнг ввел понятие «трансцендентальная функция» - это функция, объединяющая сознательное и бессознательное. В частности, трансцендентальную функцию может выполнять психоаналитик - он помогает пациенту проанализировать образы бессознательного (например, сновидения) и связать их воедино с сознательными процессами в его психике.

Как говорить

Неправильно «Я записалась на занятия по трансцендентной медитации». Правильно - «трансцендентальной».

Правильно «Когда я захожу в храм, я испытываю чувство слияния с чем-то трансцендентным».

Правильно «Искусство трансцендирует знакомые нам предметы из материального мира, наполняя их высшим смыслом».

Число называется алгебраическим , если оно является корнем некоторого многочлена с целыми коэффициентами

a n x n +a n-1 x n-1 +... +a 1 x+a 0 (т. е. корнем уравнения a n x n +a n-1 x n-1 +... +a 1 x+a 0 =0 , где a n , a n-1 , ..., a 1 , a 0 --- целые числа, n 1 , a n 0 ).

Множество алгебраических чисел обозначим буквой .

Легко видеть, что любое рациональное число является алгебраическим. Действительно, - корень уравнения qx-p=0 с целыми коэффициентами a 1 =q и a 0 =-p . Итак, .

Однако не все алгебраические числа рациональны: например, число является корнем уравнения x 2 -2=0 , следовательно, --- алгебраическое число.

Долгое время оставался нерешенным важный для математики вопрос: Существуют ли неалгебраические действительные числа? Только в 1844 году Лиувилль впервые привел пример трансцендентного (т. е. неалгебраического) числа.

Построение этого числа и доказательство его трансцендентности очень сложны. Доказать теорему существования трансцендентных чисел можно значительно проще, используя соображения об эквивалентности и неэквивалентности числовых множеств.

А именно, докажем, что множество алгебраических чисел счетно. Тогда, поскольку множество всех действительных чисел несчетно, мы установим существование неалгебраических чисел.

Построим взаимно однозначное соответствие между и некоторым подмножеством . Это будет означать, что - конечно либо счетно. Но поскольку , то бесконечно, и значит, счетно.

Пусть - некоторое алгебраическое число. Рассмотрим все многочлены с целыми коэффициентами, корнем которых является , и выберем среди них многочлен P минимальной степени (т. е. не будет корнем никакого многочлена с целыми коэффициентами меньшей степени).

Например, для рационального числа такой многочлен имеет степень 1, а для числа - степень 2.

Разделим все коэффициенты многочлена P на их наибольший общий делитель. Получим многочлен, коэффициенты которого взаимно просты в совокупности (их наибольший общий делитель равен 1). Наконец, если старший коэффициент a n отрицателен, умножим все коэффициенты многочлена на -1 .

Полученный многочлен (т. е. многочлен с целыми коэффициентами, корнем которого является число , имеющий минимально возможную степень, взаимно простые коэффициенты и положительный старший коэффициент) называется минимальным многочленом числа .

Можно доказать, что такой многочлен определяется однозначно: каждое алгебраическое число имеет ровно один минимальный многочлен.

Количество действительных корней многочлена не больше чем его степень. Значит, можно пронумеровать (например, по возрастанию) все корни такого многочлена.

Теперь всякое алгебраическое число полностью определяется своим минимальным многочленом (т. е. набором его коэффициентов) и номером, который отличает от других корней этого многочлена: (a 0 ,a 1 ,...,a n-1 ,a n ,k).

Итак, каждому алгебраическому числу мы поставили в соответствие конечный набор целых чисел, причем по этому набору восстанавливается однозначно (т. е. разным числам соответствуют разные наборы).

Пронумеруем в порядке возрастания все простые числа (нетрудно показать, что их бесконечно много). Получим бесконечную последовательность {p k } : p 1 =2 ,p 2 =3 , p 3 =5 , p 4 =7 , ... Теперь набору целых чисел (a 0 ,a 1 ,...,a n-1 ,a n ,k) можно поставить в соответствие произведение

(это число положительное и рациональное, но не всегда натуральное, ведь среди чисел a 0 , a 1 , ..., a n-1 , могут быть отрицательные). Заметим, что это число есть несократимая дробь, поскольку простые множители, входящие в разложения числителя и знаменателя, различны. Заметим также, что две несократимые дроби с положительными числителями и знаменателями равны тогда и только тогда, когда и их числители равны, и их знаменатели равны.

Рассмотрим теперь сквозное отображение:

(a 0 ,a 1 ,...,a n-1 ,a n ,k) =

Поскольку разным алгебраическим числам мы поставили в соответствие разные наборы целых чисел, а разным наборам --- разные рациональные числа, то мы, таким образом, установили взаимно однозначное соответствие между множеством и некоторым подмножеством . Поэтому множество алгебраических чисел счетно.

Так как множество действительных чисел несчетно, то мы доказали существование неалгебраических чисел.

Однако теорема существования не указывает как определить, является ли данное число алгебраическим. А этот вопрос иногда является весьма важным для математики.

Трансцендентное число — комплексное число, не являющееся алгебраическим, то есть не являющееся корнем никакого отличного от нуля многочлена с рациональными коэффициентами.

Существование трансцендентных чисел впервые установил Ж. Лиувилль в 1844 г.; он же построил первые примеры таких чисел. Лиувилль заметил, что алебраические числа не могут «слишком хорошо» приближаться рациональными числами . Именно, теорема Лиувилля гласит, что если алгебраическое число является корнем многочлена степени с рациональными коэффициентами, то для любого рационального числа справедливо неравенство

где постоянная зависит только от. Из этого утверждения следует достаточный признак трансцендентности: если число таково, что для любой постоянной существует бесконечное множество рациональных чисел, удовлетворяющих неравенствам

то трансцендентно. Впоследствии такие числа получили название чисел Лиувилля. Примером такого числа является

Другое доказательство существования трансцендентных чисел было получено Г. Кантором в 1874 г. на основе созданной им теории множеств. Кантор доказал счётность множества алгебраических чисел и несчётность множества действительных чисел, откуда следует, что множество трансцендентных чисел несчётно. Однако, в отличие от доказательства Лиувилля, эти рассуждения не позволяют привести пример хотя бы одного такого числа.

Работа Лиувилля дала начало целому разделу теории трансцендентных чисел — теории приближения алгебраических чисел рациональными или, более общо, алгебраическими числами. Теорема Лиувилля усиливалась и обобщалась в работах многих математиков. Это позволило построить новые примеры трансцендентных чисел. Так, К. Малер показал, что если — непостоянный многочлен, принимающий целые неотрицательные значения при всех натуральных, то для любого натурального число, где — запись числа в системе счисления с основанием, является трансцендентным, но не является числом Лиувилля. Например, при и получаем следующий изящный результат: число

трансцендентно, но не является числом Лиувилля.

В 1873 г. Ш. Эрмит, используя другие идеи, доказал трансцендентность неперова числа (основания натурального логарифма):

Развив идеи Эрмита, Ф. Линдеман в 1882 г. доказал трансцендентность числа, тем самым поставив точку в древней проблеме о квадратуре круга: с помощью циркуля и линейки невозможно построить квадрат, равновеликий (то есть имеющий ту же площадь) данному кругу. Более общо, Линдеман показал, что при любом алгебраическом число трансцендентно. Эквивалентная формулировка: для любого алгебраического числа, отличного от и, его натуральный логарифм является трансцендентым числом.

В 1900 г. на конгрессе математиков в Париже Д. Гильберт среди 23 нерешённых проблем математики указал на следующую, в частной форме сформулированную ещё Л. Эйлером :

Пусть и — алгебраические числа, причём трансцендентным? В частности, трансцендентны ли числа и?

Эта проблема может быть переформулирована в следующей форме, близкой к оригинальной формулировке Эйлера:

Пусть и — алгебраические числа, отличные от и, причём отношение их натуральных логарифмов иррационально. Будет ли число трансцендентным?

Первое частичное решение проблемы было получено в 1929 г. А. О. Гельфондом, который, в частности, доказал трансцендентность числа. В 1930 г. Р. О. Кузьмин усовершенствовал метод Гельфонда, в частности, ему удалось доказать трансцендентность числа. Полное решение проблемы Эйлера-Гильберта (в утвердительном смысле) было получено в 1934 г. независимо А. О. Гельфондом и Т. Шнайдером.

А. Бейкер в 1966 обобщил теоремы Линдемана и Гельфонда-Шнайдера, доказав, в частности, трансцендентность произведения произвольного конечного количества чисел вида и с алгебраическими при естественных ограничениях.

В 1996г. Ю.В. Нестеренко доказал алгебраическую независимость значений рядов Эйзенштейна и, в частности, чисел и. Это означает трансцендентность любого числа вида, где отличная от нуля рациональная функция с алгебраическими коэффициентами. Например, трансцендентной будет сумма ряда

В 1929-1930 гг. К. Малер в серии работ предложил новый метод доказательства трансцендентности значений аналитических функций, удовлетворяющих функциональным уравнениям определённого вида (впоследствии такие функции получили название функций Малера).

Методы теории трансцендентных чисел нашли применение и в других разделах математики, в частности в теории диофантовых уравнений.

В этом параграфе мы снова покинем прекрасное и уютное царство целых чисел, по которому разгуливали (чуть было не сказал - слонялись) изучая теорию сравнений. Если проследить историю возникновения и развития знаний человечества о числах, то выявится довольно парадоксальный факт - на протяжении почти всей своей многовековой истории человечество использовало на практике и пристально изучало исключительно малую долю всего множества живущих в природе чисел. Люди долгое время совершенно не подозревали о существовании, как выяснилось впоследствии, подавляющего большинства действительных чисел, наделенных удивительными и загадочными свойствами и называемых теперь трансцендентными. Судите сами (перечисляю ориентировочные этапы развития понятия действительного числа):

1) Идущая из глубины тысячелетий гениальная математическая абстракция натурального числа

Гениальность этой абстракции поражает, а ее значение для развития человечества превосходит, наверное, даже изобретение колеса. Мы привыкли к ней настолько, что перестали восхищаться этим самым выдающимся достижением человеческого разума. Однако попробуйте, для пущей достоверности представив себя не студентом-математиком, а первобытным человеком, или, скажем, студентом-филологом, сформулировать точно, что общего имеется между тремя хижинами, тремя быками, тремя бананами и тремя ультразвуковыми томографами (что общего между тремя собутыльниками мы здесь не рассматриваем). Объяснять не математику, что такое натуральное число “три” - почти безнадежная затея, однако уже пятилетний человеческий детеныш внутренне ощущает эту абстракцию и в состоянии разумно оперировать с ней, выпрашивая у мамы три конфеты вместо двух.

2) Дроби, т.е. положительные рациональные числа

Дроби естественно возникли при решении задач о разделе имущества, измерении земельных участков, исчислении времени и т.п. В древней Греции рациональные числа вообще являлись символом гармонии окружающего мира и проявлением божественного начала, а все отрезки, до некоторого времени, считались соизмеримыми, т.е. отношение их длин обязано было выражаться рациональным числом, иначе - труба (а боги этого допустить не могут).

3) Отрицательные числа и ноль (согласно некоторым научным источникам

Отрицательные числа первоначально трактовались как долг при финансовых и бартерных расчетах, однако потом выяснилось, что без отрицательных чисел и в других областях человеческой деятельности никуда не денешься (кто не верит, пусть посмотрит зимой на градусник за окном). Число ноль, на мой взгляд, первоначально служило скорее не символом пустого места и отсутствием всякого количества, а символом равенства и завершенности процесса расчетов (сколько был должен соседу, столько ему и отдал, и вот теперь – ноль, т.е. жалко).

4) Иррациональные алгебраические числа

Иррациональные числа открыли в пифагорейской школе при попытке соизмерить диагональ квадрата с его стороной, но хранили это открытие в страшной тайне – как бы смуты не вышло! В это открытие посвящались только наиболее психически устойчивые и проверенные ученики, а истолковывалось оно как отвратительное явление, нарушающее гармонию мира. Но нужда и война заставили человечество учиться решать алгебраические уравнения не только первой степени с целыми коэффициентами. После Галилея снаряды стали летать по параболам, после Кеплера планеты полетели по эллипсам, механика и баллистика стали точными науками и везде нужно было решать и решать уравнения, корнями которых являлись иррациональные числа. Поэтому с существованием иррациональных корней алгебраических уравнений пришлось смириться, какими бы отвратительными они не казались. Более того, методы решения кубических уравнений и уравнений четвертой степени, открытые в 16 веке итальянскими математиками Сципионом дель Ферро, Никколо Тартальей (Тарталья – это прозвище, означающее в переводе – заика, настоящей его фамилии я не знаю), Людовиком Феррари и Рафаэлем Бомбелли привели к изобретению совсем уж “сверхъестественных” комплексных чисел, которым суждено было получить полное признание только в 19 веке. Алгебраические иррациональности прочно вошли в человеческую практику уже с 16 века.

В этой истории развития понятия числа не нашлось места для трансцендентных чисел, т.е. чисел не являющихся корнями никакого алгебраического уравнения с рациональными или, что равносильно (после приведения к общему знаменателю), целыми коэффициентами. Правда, еще древние греки знали замечательное число p , которое, как выяснилось впоследствии, трансцендентно, но они знали его только как отношение длины окружности к ее диаметру. Вопрос об истинной природе этого числа вообще мало кого интересовал до тех пор, пока люди вдоволь и безуспешно не нарешались древнегреческой задачей о квадратуре круга, а само число p каким-то загадочным образом повылезало в разных разделах математики и естествознания.

Лишь только в 1844 году Лиувилль построил исторически первый пример трансцендентного числа, а математический мир удивился самому факту существования таких чисел. Лишь только в 19 веке гениальный Георг Кантор понял, используя понятие мощности множества, что на числовой прямой трансцендентных чисел подавляющее большинство. Лишь только в пятом параграфе этой небольшой книжки мы, наконец-то, обратим на трансцендентные числа свое внимание.

Пункт 24. Мера и категория на прямой.

В этом пункте я приведу некоторые предварительные сведения из математического анализа необходимые для понимания дальнейшего изложения. В математике придумано довольно много различных формализаций понятия “малости” множества. Нам понадобятся два из них - множества меры нуль и множества первой категории по Бэру. Оба эти понятия опираются на понятие счетности множества. Известно, что множество рациональных чисел счетно (| Q |= А 0), и что любое бесконечное множество содержит счетное подмножество, т.е. счетные множества самые “маленькие” из бесконечных. Между любым счетным множеством и множеством натуральных чисел N существует биективное отображение, т.е. элементы любого счетного множества можно перенумеровать, или, другими словами, любое счетное множество можно выстроить в последовательность. Ни один интервал на прямой не является счетным множеством. Это, очевидно, вытекает из следующей теоремы.

Теорема 1 (Кантор). Для любой последовательности { a n } действительных чисел и для любого интервала I существует точка р О I такая, что p № a n для любого n О N .

Доказательство. Процесс. Берем отрезок (именно отрезок, вместе с концами) I 1 М I такой, что a 1 П I 1 . Из отрезка I 1 берем отрезок I 2 М I 1 такой, что a 2 П I 2 и т.д. Продолжая процесс, из отрезка I n -1 берем отрезок I n М I n -1 такой, что a n П I n . В результате этого процесса получаем последовательность вложенных отрезков I 1 Й I 2 Й … Й I n Й … пересечение
которых, как известно с первого курса, непусто, т.е. содержит некоторую точку
. Очевидно, что p № a n при всех n О N .

Я не думаю, что читатели ранее не встречались с этим изящным доказательством (хотя в моей практике встречались и очень темные студенты), просто идея этого доказательства далее будет использована при доказательстве теоремы Бэра и поэтому ее полезно напомнить заранее.

Определение. Множество А плотно в интервале I , если оно имеет непустое пересечение с каждым подинтервалом из I . Множество А плотно, если оно плотно в R . Множество А нигде не плотно, если оно не плотно ни в каком интервале на действительной прямой, т.е. каждый интервал на прямой содержит подинтервал, целиком лежащий в дополнении к А .

Легко понять, что множество А нигде не плотно тогда и только тогда, когда его дополнение A ў содержит плотное открытое множество. Легко понять, что множество А нигде не плотно тогда и только тогда, когда его замыкание
не имеет ни одной внутренней точки.

Нигде не плотные множества на прямой интуитивно ощущаются маленькими в том смысле, что в них полным полно дыр и точки такого множества расположены на прямой довольно редко. Некоторые свойства нигде не плотных множеств сформулируем скопом в виде теоремы.

Теорема 2. 1) Любое подмножество нигде не плотного множества нигде не плотно.

2) Объединение двух (или любого конечного числа) нигде не плотных множеств нигде не плотно.

3) Замыкание нигде не плотного множества нигде не плотно.

Доказательство. 1) Очевидно.

2) Если A 1 и A 2 нигде не плотны, то для каждого интервала I найдутся интервалы I 1 М (I \ A 1) и I 2 М (I 1 \ A 2). Значит, I 2 М I \(A 1 И A 2), а это означает, что A 1 И A 2 нигде не плотно.

3) Очевидно, что любой открытый интервал, содержащийся в A ў , содержится также и в
.

Таким образом, класс нигде не плотных множеств замкнут относительно операции взятия подмножеств, операции замыкания и конечных объединений. Счетное объединение нигде не плотных множеств, вообще говоря, не обязано быть нигде не плотным множеством. Пример тому - множество рациональных чисел, которое всюду плотно, но является счетным объединением отдельных точек, каждая из которых образует одноэлементное нигде не плотное множество в R .

Определение. Множество, которое можно представить в виде конечного или счетного объединения нигде не плотных множеств, называется множеством первой категории (по Бэру). Множество, которое нельзя представить в таком виде, называется множеством второй категории.

Теорема 3. 1) Дополнение любого множества первой категории на прямой является плотным.

2) Никакой интервал в R не является множеством первой категории.

3) Пересечение любой последовательности плотных открытых множеств является плотным множеством.

Доказательство. Три сформулированных в теореме свойства являются по существу эквивалентными. Докажем первое. Пусть

– представление множества А первой категории в виде счетного объединения нигде не плотных множеств, I – произвольный интервал. Далее - процесс как в доказательстве теоремы Кантора. Выберем отрезок (именно отрезок, вместе с концами) I 1 М (I \ A 1). Это возможно сделать, так как в дополнении к нигде не плотному множеству A 1 внутри интервала I всегда найдется целый подинтервал, а он, в свою очередь, содержит внутри себя целый отрезок. Выберем отрезок I 2 М (I 1 \ A 2). Выберем отрезок I 3 М (I 2 \ A 3) и т.д. Пересечение вложенных отрезков
не пусто, следовательно, дополнение I \ A не пусто, а это означает, что дополнение A ў плотно.

Второе утверждение теоремы непосредственно следует из первого, третье утверждение также следует из первого, если только сделать над собой усилие и перейти к дополнениям последовательности плотных открытых множеств.

Определение. Класс множеств, содержащий всевозможные конечные или счетные объединения своих членов и любые подмножества своих членов, называется s - идеалом.

Очевидно, что класс всех не более чем счетных множеств является s -идеалом. После небольших размышлений, легко понять, что класс всех множеств первой категории на прямой также является s -идеалом. Еще один интересный пример s -идеала дает класс так называемых нуль-множеств (или множеств меры нуль).

Определение. Множество А М R называется множеством меры нуль (нуль-множеством), если А можно покрыть не более чем счетной совокупностью интервалов, суммарная длина которых меньше любого наперед заданного числа e >0 , т.е. для любого e >0 существует такая последовательность интервалов I n , что
и е Ѕ I n Ѕ < e .

Понятие нуль-множества является другой формализацией интуитивного понятия “малости” множества: нуль-множества - это множества маленькие по длине. Очевидно, что отдельная точка является нуль-множеством и что любое подмножество нуль-множества само является нуль-множеством. Поэтому тот факт, что нуль-множества образуют s -идеал вытекает из следующей теоремы.

Теорема 4 (Лебег). Любое счетное объединение нуль-множеств является нуль-множеством.

Доказательство. Пусть A i – нуль-множества, i = 1, 2, ... . Тогда для каждого i существует последовательность интервалов I ij (j =1, 2, ...) такая, что
и
. Множество всех интервалов I ij покрывает А и сумма их длин меньше e , так как
. Значит, А – нуль-множество.

Никакой интервал или отрезок не является нуль-множеством, т.к. справедлива

Теорема 5 (Гейне – Борель). Если конечная или бесконечная последовательность интервалов I n покрывает интервал I , то

S Ѕ I n Ѕ і Ѕ I Ѕ .

Я не буду приводить здесь доказательство этой интуитивно очевидной теоремы ибо его можно найти в любом мало-мальски серьезном курсе математического анализа.

Из теоремы Гейне-Бореля следует, что s -идеал нуль-множеств, подобно s -деалам не более чем счетных множеств и множеств первой категории не содержит интервалов и отрезков. Общим между этими тремя s -идеалами является также то, что они включают в себя все конечные и счетные множества. Кроме того, существуют несчетные множества первой категории меры нуль. Наиболее знакомый пример такого множества - канторово совершенное (*) множество c М , состоящее из чисел, в троичной записи которых нет единицы. Вспомните процесс построения канторова совершенного множества: отрезок делится на три равные части и средний открытый интервал выкидывается. Каждая из двух оставшихся третей отрезка снова делится на три равные части и средние открытые интервалы из них выкидываются и т.д. Очевидно, что оставшееся после этого процесса множество нигде не плотно, т.е. первой категории. Легко подсчитать, что суммарная длина выкинутых средних частей равна единице, т.е. с имеет меру нуль. Известно, что с несчетно, т.к. несчетно множество бесконечных последовательностей, состоящих из нулей и двоек (каждый элемент с представляется троичной дробью в которой после запятой идет именно последовательность из нулей и двоек).

Предлагаю читателям самостоятельно проверить, что существуют множества первой категории, не являющиеся нуль-множествами, и существуют нуль-множества, не являющиеся множествами первой категории (впрочем, если вас затруднит придумывание соответствующих примеров, не отчаивайтесь, а просто дочитайте этот пункт до теоремы 6).

Таким образом, картинка соотношений между рассматриваемыми тремя s -идеалами такова:

Итак, мы ввели два понятия малости множеств. Нет ничего парадоксального, что множество, малое в одном смысле, может в другом смысле оказаться большим. Следующая теорема неплохо иллюстрирует эту мысль и показывает, что в некоторых случаях, введенные нами понятия малости могут оказаться диаметрально противоположными.

Теорема 6. Числовую прямую можно разбить на два дополняющих друг друга множества А и В так, что А есть множество первой категории, а В имеет меру нуль.

Доказательство. Пусть a 1 , a 2 ,…, a n ,… – занумерованное множество рациональных чисел (или любое другое счетное всюду плотное подмножество R ). Пусть I ij – открытый интервал длины 1/2 i+j c центром в точке a i . Рассмотрим множества:

, j =1,2,...;

; A = R \ B = B ў .

Очевидно, что для любого e >0, можно выбрать j так, что 1/2 j < e . Тогда

,

следовательно, В – нуль-множество.

Далее,
– плотное открытое подмножество R т.к. оно есть объединение последовательности открытых интервалов и содержит все рациональные точки. Это означает, что его дополнение G j ў нигде не плотно, следовательно
– множество первой категории.

Не правда ли, удивительный результат! Из доказанной теоремы следует, что каждое подмножество прямой, оказывается, можно представить в виде объединения нуль-множества и множества первой категории. В следующем пункте мы рассмотрим конкретное разбиение R на два подмножества, одно из которых - трансцендентные числа Лиувилля - меры нуль, но второй категории по Бэру. Скорей в следующий пункт!